| Monthly Tech-Tip | No tracking! No ads! | |
A Low Cost Tester of Glaze Melt Fluidity
A One-speed Lab or Studio Slurry Mixer
A Textbook Cone 6 Matte Glaze With Problems
Adjusting Glaze Expansion by Calculation to Solve Shivering
Alberta Slip, 20 Years of Substitution for Albany Slip
An Overview of Ceramic Stains
Are You in Control of Your Production Process?
Are Your Glazes Food Safe or are They Leachable?
Attack on Glass: Corrosion Attack Mechanisms
Ball Milling Glazes, Bodies, Engobes
Binders for Ceramic Bodies
Bringing Out the Big Guns in Craze Control: MgO (G1215U)
Can We Help You Fix a Specific Problem?
Ceramic Glazes Today
Ceramic Material Nomenclature
Ceramic Tile Clay Body Formulation
Changing Our View of Glazes
Chemistry vs. Matrix Blending to Create Glazes from Native Materials
Concentrate on One Good Glaze
Copper Red Glazes
Crazing and Bacteria: Is There a Hazard?
Crazing in Stoneware Glazes: Treating the Causes, Not the Symptoms
Creating a Non-Glaze Ceramic Slip or Engobe
Creating Your Own Budget Glaze
Crystal Glazes: Understanding the Process and Materials
Deflocculants: A Detailed Overview
Demonstrating Glaze Fit Issues to Students
Diagnosing a Casting Problem at a Sanitaryware Plant
Drying Ceramics Without Cracks
Duplicating Albany Slip
Duplicating AP Green Fireclay
Electric Hobby Kilns: What You Need to Know
Fighting the Glaze Dragon
Firing Clay Test Bars
Firing: What Happens to Ceramic Ware in a Firing Kiln
First You See It Then You Don't: Raku Glaze Stability
Fixing a glaze that does not stay in suspension
Formulating a body using clays native to your area
Formulating a Clear Glaze Compatible with Chrome-Tin Stains
Formulating a Porcelain
Formulating Ash and Native-Material Glazes
G1214M Cone 5-7 20x5 glossy transparent glaze
G1214W Cone 6 transparent glaze
G1214Z Cone 6 matte glaze
G1916M Cone 06-04 transparent glaze
Getting the Glaze Color You Want: Working With Stains
Glaze and Body Pigments and Stains in the Ceramic Tile Industry
Glaze chemistry using a frit of approximate analysis
Glaze Recipes: Formulate and Make Your Own Instead
Glaze Types, Formulation and Application in the Tile Industry
Having Your Glaze Tested for Toxic Metal Release
High Gloss Glazes
Hire Us for a 3D Printing Project
How a Material Chemical Analysis is Done
How desktop INSIGHT Deals With Unity, LOI and Formula Weight
How to Find and Test Your Own Native Clays
I have always done it this way!
Inkjet Decoration of Ceramic Tiles
Is Your Fired Ware Safe?
Leaching Cone 6 Glaze Case Study
Limit Formulas and Target Formulas
Low Budget Testing of Ceramic Glazes
Make Your Own Ball Mill Stand
Making Glaze Testing Cones
Monoporosa or Single Fired Wall Tiles
Organic Matter in Clays: Detailed Overview
Outdoor Weather Resistant Ceramics
Painting Glazes Rather Than Dipping or Spraying
Particle Size Distribution of Ceramic Powders
Porcelain Tile, Vitrified Tile
Rationalizing Conflicting Opinions About Plasticity
Ravenscrag Slip is Born
Recylcing Scrap Clay
Reducing the Firing Temperature of a Glaze From Cone 10 to 6
Setting up a Clay Testing Program in Your Company
Simple Physical Testing of Clays
Single Fire Glazing
Soluble Salts in Minerals: Detailed Overview
Some Keys to Dealing With Firing Cracks
Stoneware Casting Body Recipes
Substituting Cornwall Stone
Super-Refined Terra Sigillata
The Chemistry, Physics and Manufacturing of Glaze Frits
The Effect of Glaze Fit on Fired Ware Strength
The Four Levels on Which to View Ceramic Glazes
The Majolica Earthenware Process
The Potter's Prayer
The Right Chemistry for a Cone 6 MgO Matte
The Trials of Being the Only Technical Person in the Club
The Whining Stops Here: A Realistic Look at Clay Bodies
Those Unlabelled Bags and Buckets
Tiles and Mosaics for Potters
Toxicity of Firebricks Used in Ovens
Trafficking in Glaze Recipes
Understanding Ceramic Materials
Understanding Ceramic Oxides
Understanding Glaze Slurry Properties
Understanding the Deflocculation Process in Slip Casting
Understanding the Terra Cotta Slip Casting Recipes In North America
Understanding Thermal Expansion in Ceramic Glazes
Unwanted Crystallization in a Cone 6 Glaze
Using Dextrin, Glycerine and CMC Gum together
Volcanic Ash
What Determines a Glaze's Firing Temperature?
What is a Mole, Checking Out the Mole
What is the Glaze Dragon?
Where do I start in understanding glazes?
Why Textbook Glazes Are So Difficult
Working with children
Glaze Chemistry Basics - Formula, Analysis, Mole%, Unity
Description
Part of changing your viewpoint of glazes, from a collection of materials to a collection of oxides, is learning what a formula and analysis are, how conversion between the two is done and how unity and LOI impact this.
Article
Most have traditionally thought of glazes exclusively in terms of their batch recipe of powdered ceramic minerals and materials. However, the kiln decomposes these materials down to their basic building blocks (called oxides). On cooling a new form of matter is created: a glass built from a structure of the oxide molecules contributed by the materials. Since each oxide contributes specifically to the physical properties of the glass (e.g. melting temperature, thermal expansion, surface character, color, index of refraction, etc) we can say there is a direct relationship between chemistry and fired glaze properties. This suggests looking at glazes from two different levels, as appropriate: recipe or chemistry.
Absolute fired properties (e.g. expansion and melting behavior) can often be predicted from an oxide formula (assuming all the materials go into solution in the melt). Formulas routinely draw from ten or fewer oxides, each of which has well-documented fired property contributions. Recipes, by comparison, are complex because they draw on hundreds of materials, each of which can source many oxides.
Sometimes it is clear whether a problem should be analyzed at the recipe or formula level, other times it is not. For example, the oxide formula of a fired body has nothing to do with its plasticity, texture or even its maturity and color. By contrast, adjusting the firing temperature of a glaze is an ideal problem to approach at the formula level: SiO2 is the glass, Al2O3 a melt stabilizer and there are half a dozen fluxing oxides to melt them (the concentration and mix of which determines the temperature). Adjusting thermal expansion to stop crazing is another problem for the formula level. The fluxing oxides have clearly-defined expansion values and it is normally obvious how to change a formula to reduce expansion. This is just about impossible to do on the recipe level without affecting the fired glaze appearance (because materials supply multiple oxides).
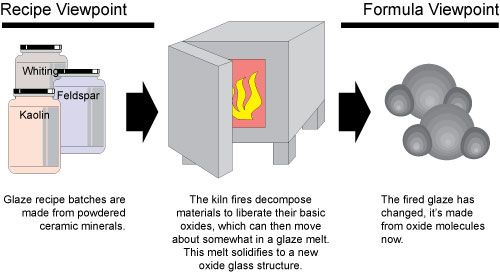
There are many times when a mixed viewpoint is necessary. Consider converting a glaze to a slip for use in single-fire. Such glazes need a much higher percentage of clay (or more plastic clays). It will often be a matter of sourcing more Al2O3 from the plastic clays you decide to use instead of from feldspars. And then sourcing the lost feldspar-supplied KNaO from an alkali frit. Like this scenario, you almost always need to approach on both the oxide and recipe levels. This is because the points when recipe adjustments to a glaze significantly influence the oxide formula, or, where oxide level adjustments alter the physical properties are almost always crossed.
Atoms, Molecules and Oxides
For practical purposes here, we can consider atoms to be the most basic building blocks of matter. Atoms insist on bonding with others to form molecules. The 15 or so types useful in ceramics like to combine with oxygen to form oxides (e.g. SiO2, CaO). It normally takes a nuclear reaction to tear an atom apart, but molecules can be dissected and rearranged with the kinds of chemical reactions that occur as a result of melting in a kiln, it can decompose complex molecules (e.g. feldspar K2O · Al2O3 · 6SiO2 ) into the three basic oxides.
The kiln works its magic by juggling oxide molecules around to combine with each other in infinite ways. The time and temperatures provided determine the extent to which the breakdown (decomposition) and subsequent reconstruction occurs. During this decomposition, some gases are liberated (e.g. CO2, SO4 , CO, etc.). Much effort has been applied to predicting what kiln fires will do with given mixtures of oxide molecules. A basis for understanding this has been the classification of oxides into a three-group model. Each group contributes definite properties. Each group exists in certain proportions for each glaze type and firing temperature. Individual oxides also impart special properties when they predominate in their group or when they exist in critical proportions with other selected oxides.
Another important factor in the development of understanding what oxide mixtures will do in the kiln has been standardization in the way a mix of oxide molecules is expressed. Two primary standards are important.
The Formula
A formula expresses an oxide mix according to the relative numbers of molecule types, it is ideal for analyzing and predicting properties of a fired glaze or glass. This is because the formula gives us an idea about the molecular structure responsible for the fired behavior. Since the kiln builds these oxide molecules one by one into a structure, it follows that one will never really "understand" a glaze till seeing its oxide formula.
A formula is flexible. We can arbitrarily retotal it without affecting the relative numbers of oxide molecules. In fact, this is standard procedure to produce a "unity formula" (more in a minute). With a formula, you need not worry whether there is 1 gram, 1 ton, or one billion molecules, only relative numbers matter (it is thus allowable to express a formula showing molecule parts e.g. 0.4 MgO).
An Example of a Formula
| Fluxes | Intermediates | Glass Formers | |||
|---|---|---|---|---|---|
| RO | R2O3 | RO2 | |||
| K2O | 0.6 | Al2O3 | 0.9 | SiO2 | 9.0 |
| CaO | 1.3 | ||||
| MgO | 0.2 | ||||
| ZnO | 0.1 | ||||
Notice in the above grouping: the bases, acids, and amphoterics or simply the RO, R2O3, and RO2 oxides (where "R" is the element combining with oxygen). The right column has the greatest oxygen component, the left has the least. Simplistically, we can view these three groups as the silica:alumina:fluxes system. This latter convention is not really correct because there are more glass builders than SiO2, other intermediates besides Al2O3, and the ROs do more than just flux. But because this method evokes immediate recognition, let's use it anyway (ancient potters referred to these three as the blood, flesh, and bones of a glaze, not a bad way to think of it).
All formulas have their specific calculated formula weights (a matter of simple addition of atomic weights). The following chart shows how oxide weights are derived and how a formula weight is calculated from an existing formula.
Calculating the Formula Weight
-----------------------------------------------------------------
Atoms Num *wt Formula to
in of of Total Oxide Calculate
Oxide Oxide Each Atom Wt Wt Weight For
-----------------------------------------------------------------
K2O K 2 x 39.1 = 78.2
O 1 x 16 = 16 = 94.2 x 0.60 = 56.5
CaO Ca 1 x 40.1 = 40.1
O 1 x 16 = 16 = 56.1 x 1.30 = 72.9
MgO Mg 1 x 24.3 = 24.3
O 1 x 16 = 16 = 40.3 x 0.20 = 8.1
ZnO Zn 1 x 65.4 = 65.4
O 1 x 16 = 16 = 81.4 x 0.10 = 8.1
Al2O3 Al 2 x 26.9 = 53.8
O 3 x 16 = 48 =101.8 x 0.90 = 91.6
SiO2 Si 1 x 28.1 = 28.1
O 2 x 16 = 32 = 60.1 x 9.00 = 540.9
-----------------------------------------------------------------
*Data from Appendix of many textbooks Formula Wt 778.2
These weights are not grams; they are atomic weight units. They compare the weight of a molecule of the oxide with an atom of hydrogen. CaO weighs 56.1 because Ca (calcium) weighs 40.1 and O (oxygen) weighs 16. This means only that CaO is 56.1 times heavier than a single atom of benchmark hydrogen. Al2O3 (alumina oxide) is 102 times heavier; so for each weight unit it will yield fewer molecules than CaO.
The Unity Formula
The three-column format of expressing a formula was first used by Hermann Seger and today it is still called the "Seger Formula". Such formulas are normally 'unified', that is, all the numbers are scaled so that the RO column totals one (if RO oxides are lacking the R2O3 column is unified). A formula thus said to be "unified on the fluxes" or "set to RO unity". Unity formulas are a 'standard', so one can be compared to another.
The following chart takes the above formula (which had Al2O3 unity) and recalculates to 'flux unity'. The expression "bring the fluxes to unity" means "make the fluxes add up to one".
Adjusting a Formula to Flux Unity
---------------------------------
Raw Unity
Oxides Formula Formula
---------------------------------
K2O 0.6 / 2.20 = 0.3
CaO 1.3 / 2.20 = 0.6
MgO 0.2 / 2.20 = 0.1
ZnO 0.1 / 2.20 = 0.0
----- -----
Flux total 2.2 1.0
Al2O3 0.9 / 2.20 = 0.4
SiO2 9 / 2.20 = 4.1
---------------------------------
Adjusting unity is rather like calculating percentages.
This format is suitable for expressing all glazes and many materials. However, refractory clays expressed as a formula will, by necessity, be shown with unity on the R2O3 column because they may have little or no flux. Other materials may have nothing but fluxing oxides, so one or all can be unified.
Mole Percent
The Mole Percent (Mole%) calculation type has become popular because it provides room to rationalize oxide identity, interplay, concentration, and firing temperature. Here are some reasons why:
- The Seger unity model does not work well at lower temperatures. Some oxides that are powerful fluxes at high temperatures are refractory in low fire. Dynamic reassignment of oxides to the Seger groups by temperature is not practical at this time.
- Oxides have a much more individual presence than the Seger method tends to recognize. Their contributions to particular properties often are not linear according to concentration. Thus a more complex understanding of concentration vs. effect is needed.
- Oxide interplay producing characteristics attributable to the group is not recognized by the Seger system.
- Boron is both a glass and a flux and the logic for its employment at various temperature ranges differs. It does not 'plug into' a Seger formula very well.
Mole% is a calculation of the percentage of oxide molecules by number (an analysis compares their weights). Here is the method used to convert a raw formula to a Mole% formula.
Raw Mole
Oxides Formula Percent
------------------------------------
K2O 0.6 / 12.1 x 100 = 5.0%
CaO 1.3 / 12.1 x 100 = 10.7
MgO 0.2 / 12.1 x 100 = 1.7
ZnO 0.1 / 12.1 x 100 = 0.8
Al2O3 0.9 / 12.1 x 100 = 7.4
SiO2 9.0 / 12.1 x 100 = 74.3
----- -----
Total 12.1 100.0
-----------------------------------
Mole% ignores LOI as do formulas, it just looks at the oxides that makeup the fired glass.
The Percentage Analysis
An "analysis" compares oxides by the weights of their molecules, not the numbers of molecules. It is important to note that an analysis comparison between two glazes can look quite different from a Mole% comparison since oxide molecule weights differ greatly.
Consider this example:
| Formula | Analysis | |
| CaO | 0.04 | 0.1% |
| MgO | 0.03 | 0.1% |
| K2O | 0.61 | 2.9% |
| Na2O | 0.29 | 0.9% |
| Fe2O3 | 0.03 | 0.3% |
| TiO2 | 0.10 | 0.4% |
| Al2O3 | 4.52 | 23.7% |
| SiO2 | 23.27 | 71.6% |
If you are not sure of the difference between an analysis and formula yet, think of a can of mixed nuts. It may contain cashews, brazils, peanuts, almonds and filberts. The label may specify the percentage of each type of nut in the mix. A mixture of 30% peanuts has 30% peanuts by weight. Think of that as an analysis. When you open the can you may be surprised to find many more peanuts than expected. This is because peanuts are the smallest and therefore the lightest, so even though they make up only 30% by weight, they may well outnumber all the others combined. If you actually sorted and counted them, the resultant ratio would be like a formula.
The analysis format is best suited to showing how much of each individual oxide is in a mix. For example, feldspars are used as a source of flux, although they also provide SiO2 and Al2O3 , so a buyer wants to know how much flux each brand has. A percentage analysis figure shows this, whereas a formula figure does not. An individual item can be extracted from an analysis (e.g. 10% K2O) and it is meaningful. However, an individual item in a formula is only significant in the context of other amounts in that formula.
An analysis provides flexibility in allowing the inclusion of organics, water, and additives that are burned away during firing. For example, if a material loses 10% weight on firing, we can just say LOI (Loss on Ignition) is 10%. However, it would be difficult to express this 10% loss in a formula. Strictly speaking, a formula cannot have an LOI because it expresses the mix of oxides in a fired ceramic. It is no surprise then that the analysis has become a standard used to express the make-up of raw glaze and clay materials on manufacturers data sheets.
You might have noticed that many, in fact most published analyses do not total exactly 100. There are a variety of reasons for this. It is common for the LOI to be wrong because it does not include all of the volatile materials (even moisture in the sample). Also, labs typically measure the amount of a specific group of oxides, others that are not checked for are not included in the total (most raw materials, especially clays, contain trace amounts of dozens of elements). The amounts of some oxide types are more difficult to quantify and their numbers are thus not as accurate. The fact that companies do not attempt to account for every last half percent of material is generally an admission that the science of practical inexpensive chemical analysis is not exact.
Some people are critical of the use of the formula because it can be very misleading in comparing amounts of a specific oxide in different formulations. To illustrate, consider comparing a pure feldspar with a typical cone 6 transparent glaze recipe.

Desktop INSIGHT showing formula and analysis side-by-side
Desktop Insight was the first to enable users to compare two recipes and their formulas side-by-side and interactively update when recipe changes were made. It also enabled users to show formulas and analyses side-by-side.
The formula on the lower right makes it appear that there is more than twice as much silica and three times as much alumina in the feldspar. However in the analysis on the left there is only a little more silica and much less than twice as much alumina. This all relates to the difference in weight of various oxide molecules (refer back to the mixed nut analog used above to rationalize this). Another criticism of formulas in favor of the analysis is that having 1% iron in a body or glaze makes more sense than, for example, 0.05 in the formula. There is a lot of merit in this observation, and most technicians rationalize the effects of coloring and opacifying oxides in terms of their percentage in the analysis, often not even considering them in formula comparisons. However these observations are in no way an indication that formulas are useless. Formulas are very useful as long as you are comparing two similar mixtures (e.g. two cone 6 glazes using similar materials).
Loss On Ignition (LOI)
The primary purpose of recipe calculations is to derive the formula for the glass that comes out of the kiln, from the mix of recipe materials that go into the kiln. A fired glass has no organics or carbonates; so it always has zero LOI. This means that LOI is never shown for a glaze formula and you will never need to worry about it for any batch-to-formula or analysis calculations.
However, many raw materials that go into the kiln do lose weight during firing; so they are not sourcing as many oxide molecules as a calculation might suggest. If a raw material loses weight on firing, it must be accounted for in calculations. This weight loss could be illustrated with the child and his LEGOblocks already considered. While disassembling existing structures to free up all blocks, he may discard a number that do not lend themselves to inclusion in the intended project. You can think of LOI as being like the shells we throw away from a bag of nuts.
We compensate for anything lost during firing by increasing the formula weight. For example, 100 grams of kaolin going into a kiln produces only 88 grams of oxides for glass making. By increasing the formula weight of the kaolin by the correct amount, a full calculated oxide yield will result. By increasing the formula weight of the kaolin by the correct amount, a full calculated oxide yield will result. Insight-live.com stores a material's analysis in its materials database exactly as you enter it. Of course you need to enter the LOI as part of the analysis. Since it knows the LOI for each material in a recipe, it can calculate the LOI of the raw recipe as a whole. This can be very useful
If you have an analysis lacking an LOI figure or suspect the accuracy of the analysis delivered by a lab, then you can weigh, fire, and weigh again to derive the LOI and compensate the analysis.
Following is a method of applying a 5% measured LOI to an existing analysis. This is called "LOI Compensating an Analysis".
LOI Compensating an Analysis
100 - 95 = 5 / 100 = 0.95
-------------------------------
K2O 7.3% x 0.95 = 6.9%
CaO 9.4% x 0.95 = 8.9%
MgO 1.0% x 0.95 = 1.0%
ZnO 1.0% x 0.95 = 1.0%
Al2O3 11.8% x 0.95 = 11.2%
SiO2 69.5% x 0.95 = 66.0%
LOI 0.05 5.0%
-------------------------------
100.0% 100.0%
Converting Between Formula & Analysis
In a formula the number of and weight of each oxide molecule are known; so it is just a matter of multiplying these amounts and adding the results to get the total weight. Next, the analysis can be derived by dividing each product by the total weight and multiplying by 100 as shown in the following spreadsheet fragment.
Converting a Formula to an Analysis
Oxides Formula Weights
---------------------------------------------------
K2O 0.27 x 94.2 = 25.43 / 353.78 = 7.19%
CaO 0.59 x 56.1 = 33.10 / 353.78 = 9.36%
MgO 0.09 x 40.3 = 3.63 / 353.78 = 1.03%
ZnO 0.05 x 81.4 = 4.07 / 353.78 = 1.15%
Al2O3 0.41 x 101.8 = 41.74 / 353.78 = 11.80%
SiO2 4.09 x 60.1 = 245.81 / 353.78 = 69.48%
---------------------------------------------------
Formula Weight 353.78
In an analysis the percentage of each oxide type is known; so dividing these by the molecule weights will produce a raw formula. This can then be unity adjusted. The following spreadsheet fragment demonstrates this.
Converting an Analysis to a Formula
Unity
Oxides Analysis Weights Formula
---------------------------------------------------
K2O 7.19% / 94.2 = 0.0763 / .2827 = 0.27
CaO 9.36% / 56.1 = 0.1668 / .2827 = 0.59
MgO 1.03% / 40.3 = 0.0254 / .2827 = 0.09
znO 1.15% / 81.4 = 0.0141 / .2827 = 0.05
------
0.2827
Al2O3 11.80% / 101.8 = 0.1159 / .2827 = 0.41
SiO2 69.48% / 60.1 = 1.1561 / .2827 = 4.09
---------------------------------------------------
Theoretical and Actual Formulas
If a totally pure source of kaolin could be found, it would have a formula of Al2O3 · 2SiO2 . No real deposit in the world has this, but most are close. It has, therefore, been the custom to use a theoretical formula when using kaolin in calculations (since the error introduced is small). this principle applies to most standard materials such as feldspar, whiting, dolomite, talc, etc.)."
However, the error involved with some theoretical formulas can border on unacceptable if the type of material used is not as pure as the formula suggests. this is more serious if different mixtures being compared are using different types or brand names of a material like feldspar, or if a calculation is being done in order to substitute a similar but not identical material into a recipe. It becomes necessary to use a more precise formula, which although more complicated will yield a better calculation. The manufacturer's data sheet is the best source of information on a material's formula.
Notice the differences in the following generic and name-brand feldspars.
| G-200 FELDSPAR | GENERIC POTSPAR | CUSTER FELDSPAR | ||||
| CaO | 0.81% | 0.08 | 0.30% | [ 0.03] | ||
| K2O | 10.75% | 0.63 | 16.92% | 1.00 | 10.28% | [ 0.68] |
| MgO | 0.05% | 0.01 | ||||
| Na2O | 3.04% | 0.27 | 2.91% | [ 0.29] | ||
| Al2O3 | 18.50% | [ 1.00] | 18.32% | [ 1.00] | 17.35% | [ 1.05] |
| SiO2 | 66.30% | 6.08 | 64.76% | 6.00 | 69.00% | 7.11 |
| Fe2O3 | 0.08% | 0.00 | 0.12% | 0.01 | ||
| LOI | 0.16% | 0.04% | ||||
Related Information
Ceramic Oxide Periodic Table

Pretty well all common traditional ceramic base glazes are made from less than a dozen elements (plus oxygen). Go to the full picture of this table and click or tap each of the oxides to learn more (on its page at digitalfire.com). When materials melt, they decompose, sourcing these elements in oxide form. The kiln builds the glaze from them, it does not care what material sources what oxide (assuming, of course, that all materials do melt or dissolve completely into the melt to release those oxides). Each of these oxides contributes specific properties to the glass. So, you can look at a formula and make a good prediction of the properties of the fired glaze. And know what specific oxide to increase or decrease to move a property in a given direction (e.g. melting behavior, hardness, durability, thermal expansion, color, gloss, crystallization). And know about how they interact (affecting each other). This is powerful. A lot of ceramic materials are available, hundreds - that is complicated when individual materials source multiple oxides. Viewing a glaze as a simple unity formula of ceramic oxides is just simpler.
Links
| Projects |
Oxides
|
| URLs |
https://digitalfire.com/services/database.php?list=labs
Laboratories who can can do a chemical analysis on a material |
| Glossary |
LOI
Loss on Ignition is a number that appears on the data sheets of ceramic materials. It refers to the amount of weight the material loses as it decomposes to release water vapor and various gases during firing. |
| Glossary |
Oxide Formula
In ceramics, the chemistry of fired glazes is expressed as an oxide formula. There are direct links between the oxide chemistry and the fired physical properties. |
| Glossary |
Glaze Chemistry
Glaze chemistry is the study of how the oxide chemistry of glazes relate to the way they fire. It accounts for color, surface, hardness, texture, melting temperature, thermal expansion, etc. |
| Glossary |
Unity Formula
The chemistry of ceramic glazes are normally expressed as formulas. A unity formula has been retotaled to make the numbers of flux oxides total one. |
| By Tony Hansen Follow me on        |  |
Got a Question?
Buy me a coffee and we can talk

https://digitalfire.com, All Rights Reserved
Privacy Policy
